¿Qué es un conjunto?
El concepto de conjunto no se define
pero entendemos que un es conjunto la reunión o colección de objetos con
características comunes.
Los objetos pertenecientes al
conjunto reciben el nombre de elementos o miembros del conjunto.
Por lo regular se utilizan llaves
para reunir a los elementos del conjunto. Los elementos dentro de las llaves se
escriben separados por comas.
Se utilizan letras mayúsculas para representar
o nombrar a los conjuntos.
Elemento es cada uno de los objetos
por los cuales está conformado un conjunto.
Por ejemplo, para los ejemplos
tomados anteriormente en el concepto de conjunto. Luis, Antonio, Paula, son los
elementos del primer conjunto, porque ellos son alumnos de colegio. 1, 3,5 son
elementos del segundo conjunto porque son números impares.
¿Cuáles son las formas de determinar un conjunto?
Un conjunto puede determinarse de dos
formas:
-Por extensión: escribiendo
dentro de una llave los nombres de los elementos del conjunto.
-Por comprensión: escribiendo dentro de una llave una propiedad característica de los
elementos del conjunto y solamente de ellos.
Ejemplo: El conjunto de los meses del
año se nombra:
-Por extensión: {Enero, febrero, marzo, abril, mayo, junio, julio, agosto,
septiembre, octubre, noviembre, diciembre}
-Por comprensión: {meses del año}, o bien, de esta otra forma: {x/x es un mes del
año}, que se lee: conjunto de elementos x tales que x es un mes del año.
Ejemplo: El conjunto dedos de la mano
se nombra
-Por extensión: {Pulgar, Indicé, Mayor, Anular, meñique}
-Por comprensión: {dedos de la mano}, o bien, de esta otra forma: {x/x es dedo de la
mano}, que se lee: conjunto de elementos x tales que x es un dedo de la mano
¿Qué es la relación de pertenencia?
¿Qué es la relación de pertenencia?
Es la relación que existe entre un
elemento y un conjunto, así, un elemento pertenece al conjunto, y se representa
de esta forma.
Ejemplo, A = {x/x es dedo de la mano}
B= índice, entonces
B
A
Cuando un elemento no está en el
conjunto dicho elemento no pertenece al conjunto, y se representa de la siguiente
manera
Ejemplo, A = {x/x es mes del año}
B= índice, entonces
B
A
Diagrama de Venn
Un Diagrama de Venn es una
representación gráfica, normalmente óvalos o círculos, que nos muestra las
relaciones existentes entre los conjuntos. Cada óvalo o círculo es un conjunto
diferente. La forma en que esos círculos se sobreponen entre sí muestra todas
las posibles relaciones lógicas entre los conjuntos que representan. Por
ejemplo, cuando los círculos se superponen, indican la existencia de
subconjuntos con algunas características comunes
1.-Observa que en nuestro caso usamos
cuadrados en lugar de círculos, esto lo hacemos para facilitar los cálculos en
nuestra aplicación. A continuación tienes un ejemplo de un diagrama.
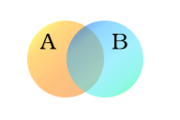2.- Fíjate que hay tres zonas en el
diagrama: Una donde solo hay elementos de A, otra donde solo hay elementos de
B, y una tercera donde están los elementos comunes a ambos conjuntos.
3.- Coloca en cada zona los elementos
de los conjuntos A y B que se muestran.
4.- Representa en tu cuaderno tres
diagramas que hayas logrado realizar correctamente. (Diagrama y conjuntos por
extensión)
-Los diagramas de Venn son una forma
para representar gráficamente conjuntos, subconjuntos, intersecciones,
y uniones.
Operaciones con conjuntos
Sean A y B conjuntos.
La unión de los conjuntos A y B es el conjunto, denotado por A U B,
formado por los elementos que estén en al menos uno de los conjuntos A o B.
Este conjunto, expresado por comprensión es:
A U B = {x E U /
x E A ˅ x E B}
Así, podemos decir que los elementos
de la unión del conjunto A con el conjunto B son aquéllos que estén o bien en A
o en B o en ambos.
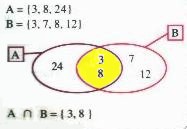
En la figura de la derecha, está
señalado en verde el conjunto A U B.
Conjunto A = {3, 8, 24}
Conjunto B = {13, 7, 8, 12}
Los elementos que se repiten entre A
y B son: 3 y 8. Estos elementos se anotan en la parte de color amarillo pues
representa el lugar común entre ambos conjuntos.
Otro
ejemplo:
B = { a, b, c, d, e, f }
C = {
a, d, f, g, h }
B C =
U{a, d, f }
En el diagrama de Venn la parte
ennegrecida representa la intersección de B y C.
Unión de conjuntos: La unión de dos o más conjuntos es otro conjunto
formado por los elementos que pertenecen a uno u otro conjunto o a ambos.
La unión se
representa por el símbolo U Si un elemento está repetido, se coloca
una sola vez.
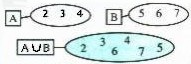Cuando no
hay elementos comunes o repetidos (esquema 1) se anotan todos los elementos en
un solo conjunto (una sola figura cerrada):
A U B
= {2, 3, 4, 5, 6, 7}.
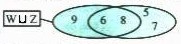Si hay
elementos repetidos, éstos se anotan en la zona común a ambos
conjuntos (esquema 2), donde se juntan ambas figuras cerradas:
W U Z
= {9, 6, 8, 5, 7}.
Aplicaciones
Teoría de conjuntos generalizada
La teoría de conjuntos generalizada
es una teoría axiomática, y su fácil modificación permite aplicarla a átomos
sin estructura interna. Los conjuntos tienen tanto conjuntos como elementos, y
también tienen átomos como elementos. La teoría de conjuntos generalizada se
aplica a pares ordenados y pares no ordenados que tengan estructura interna.
Teoría de hiperconjuntos
Teoría de conjuntos constructiva
La teoría de conjuntos constructiva
sustituye la lógica clásica con lógica intuitiva. En la teoría de conjuntos
axiomática, si los axiomas no-lógicos son formulados de manera precisa, la
aplicación de la teoría de conjuntos se conoce como Teoría de Conjuntos
Intuitiva. Esta teoría funciona como un método teórico de conjuntos para
abordar campos constructivos de la matemática.
-Para
organizar diferentes objetos y situaciones de nuestra vida cotidiana.
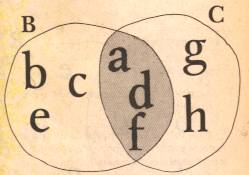
No hay comentarios:
Publicar un comentario