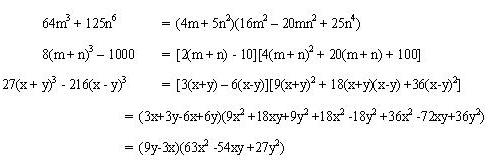Casos de factorizacion (4,5,6)

Casos de Factorización

Cuarto caso (trinomio de la forma x2+bx+c):

Este tipo de trinomio tiene las siguientes características:

• Tienen un término positivo elevado al cuadrado y con coeficiente 1 (x2).

• Posee un término que tiene la misma letra que el termino anterior pero elevada a 1 (bx) (puede ser negativo o positivo).

• Tienen un término independiente de la letra que aparece en los otros dos (+ o -).

Reglas para factorizar un trinomio de esta forma:

1.     Se descompone el trinomio en dos factores binomios cuyo primer término será la raíz cuadrada del término x2.

2.     El signo del primer binomio será el mismo signo que tenga el término “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.

3.     Si los dos factores tienen signos iguales entonces se buscan dos números cuya suma sea igual que el valor absoluto del factor “b” de “bx”, y cuyo producto sea igual al valor absoluto del factor “c”, estos números son los segundos términos de los factores binomios.

4.     Si los dos factores tienen signos diferentes entonces se buscan dos números cuya diferencia sea igual que el valor absoluto del factor “b” de “bx”, y cuyo producto sea igual al valor absoluto del factor “c”, el mayor de estos números será el segundo término del primer factor binomio, y el menor de estos números será el segundo término del segundo factor binomio.

Ejemplo explicativo:

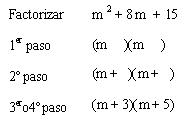
Ejemplos:

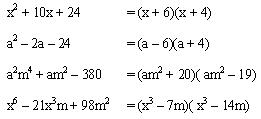
Detengámonos un poco en los últimos dos ejemplos.

En el tercero podemos ver que lo que hemos llamado “x” no es una sola letra, pero aun así se utiliza el mismo procedimiento, esto es porque el “x” es un factor lo que implica que no necesariamente será una simple letra, este puede ser también un polinomio completo.

Siguiendo con el tercero vemos su cantidad numérica es bastante elevada y no todos pueden ver fácilmente los números que buscamos, una herramienta bastante útil es descomponer este número en sus factores primos, de esta manera sabemos que cualquier combinación que hagamos al multiplicar estos números para formar los dos que busco cumplirán con el requisito multiplicativo y solo me preocupare por cumplir la suma algebraica. Así:

En el cuarto ejemplo se observa que el término “c” no es un simple numero sino que tiene una forma “cx2”, en este caso no se ha hecho ninguna diferencia simplemente se ha tomado como factor “b” como si fuera “21m” así al multiplicar (7m)(14m) nos resulta 98m2  y al sumar 7m + 14m nos da 21m, con lo que se cumple con los requisitos.

Los términos “x”, “b” y “c” pueden ser cualquier cosa, ya sea números, letras, o polinomios, solo se necesita que se cumplan las reglas indicadas.

Quinto caso (trinomio de la forma ax2+bx+c):

Este tipo de trinomio se diferencia del anterior debido a que el término al cuadrado (x2) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:

1.     Multiplicamos el coeficiente “a” del factor “ax2” por cada termino del trinomio, dejando esta multiplicación indicada en el término “bx” de la manera “b(ax)”, y en el término “ax2” de la manera . “ax2”

2.     Se descompone el trinomio en dos factores binomios cuyo primer término será la raíz cuadrada del término “ax2” la que sería “ax”.

3.     al producto resultante lo dividimos entre el factor “a”, con el fin de no variar el valor del polinomio.

4.     El signo del primer binomio será el mismo signo que tenga el término “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.

5.     Se buscaran los segundos términos de los binomios según los pasos tres y cuatro del caso del trinomio anterior.

Ejemplo explicativo:

Ejemplos:

Siempre que sea posible hay que realizar la división indicada que nos queda de este tipo de trinomio, sin olvidar que cada factor del denominador que se simplifique se corresponde (2.3.5) a todos los términos de uno solo de los binomios.

Sexto caso (suma de cubos):

Recordamos de cocientes notables que:

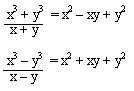
Pero en la división exacta el dividendo es igual al divisor multiplicado por el cociente, efectuándolo nos queda:

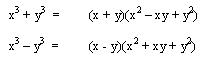
De donde se deducen las siguientes reglas:

• La suma de dos cubos perfectos se descompone en dos factores, el primero es la suma de sus raíces cúbicas, y el segundo se compone de el cuadrado de la primera raíz menos el producto de ambas raíces más el cuadrado de la segunda raíz.

• La diferencia de dos cubos perfectos se descompone en dos factores, el primero es la diferencia de sus raíces cúbicas, y el segundo se compone del cuadrado de la primera raíz más el producto de ambas raíces mas el cuadrado de la segunda raíz.

Ejemplo explicativo:

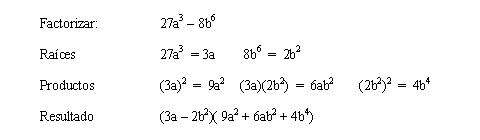
Ejemplos:

Factorizacion

Factorización

Primer caso(monomio):

En álgebra, un monimio se considera un único término numérico. Dos monomios constituyen un polinomio o binomio. Sacar el factor común de un monomio es bastante fácil, y ha de aprenderse antes de intentar factorizar un polinomio. Cuando estudies álgebra, se te pedirá que sepas factorizar un monomio antes que cualquier otro término.

Instrucciones

1 Determina cómo factorizar un número. Factoriza un número dado, como el 24. Para factorizar el 24, encuentra dos múltiplos o números que, cuando se multipliquen, den 24.

2 Utiliza los números 6 y 4. Al multiplicar estos dos números, obtienes 24. Ahora factoriza el 6 mediante la búsqueda de dos múltiplos que den como resultado 6. Usemos el 2 y el 3. Entonces busca múltiplos de 4; 2 y 2. Al final, habrás factorizado 24 con los múltiplos de 6 (2, 3) y de 4 (2, 2).

3 Encuentra el factor común. En este ejemplo, el factor común entre las dos series de múltiplos (6 y 4) es 2. Dado el ejemplo de 24, los monomios son 2, 2, 2 y 3. También puede escribirse como 2*2*2*3 o como 3*2^3.

4 Factoriza una expresión usando letras. Si tienes un número seguido de x^2, entonces la x se ha de sacar dos veces y tendrá este aspecto: x*x.

Ejemplos:

Ejemplo. Factorizar el monomio 24xy³z².

24xy³z² = 2 • 2 • 2 • 3 • x • y • y • y • z

Ejemplo. Factorizar el monomio -35a³b.

-35a³b = -1 • 5 • 7 • a • a • a • b

Se pretende descomponer en factores la expresión algebraica:  ax+a .Como  los factores de la expresión ax+a  son ax  y  a , los cuales tienen en común a  a escribiremos al factor común a como coeficiente de la expresión x+1  teniendo  en cuenta  ax + a= a(x+1)

 

Segundo caso(diferencia de cuadrados):

EJEMPLO 1: (Fácil)

x² - 9 = (x + 3).(x - 3)

x     3

Los dos términos son cuadrados. Las "bases" son x y 3. Se factoriza multiplicando la "suma de las bases" por la "resta de las bases".

EXPLICACIÓN:

Es una resta de dos términos que son cuadrados:

x² es el cuadrado de x

9 es el cuadrado de 3

1) "Bajo las bases", como hacía en el Tercer Caso. Las bases son: x y 3). Esto es simplemente una anotación, y no forma parte de la factorización. Pero es mejor ponerlo, para que el profesor vea que entendemos lo que estamos haciendo.

2) Pongo esas bases sumando y restando, entre paréntesis y multiplicándose. El resultado de la factorización es entonces:

(x + 3).(x - 3)         SUMA POR RESTA DE LAS BASES

Es decir: "Las bases sumadas, multiplicado por la bases restadas".

Ejemplos:

EJEMPLO 2: (Con dos letras)

x² - y² = (x + y).(x - y)

x     y

Las dos bases son letras 

EJEMPLO 3: (Con el "1")

b² - 1 = (b + 1).(b - 1)

b     1

No hay que olvidar que el número 1 es un cuadrado.

EJEMPLO 4: (Con fracciones)

x² - 9/25 = (x + 3/5).(x - 3/5)

x      3/5

9/25 es cuadrado. Porque 9 es cuadrado (de 3), y 25 también (de 5)

EJEMPLO 5: (Con potencias distintas de 2)

x⁶ - 4 = (x³ + 2).(x³ - 2)

x³   2

x⁶ es también un cuadrado, es el cuadrado de x³. Ya que (x³)² es igual a x⁶

EJEMPLO 6: (Con términos "compuestos")

36x² - a⁶b⁴ = (6x + a³b²).(6x - a³b²) 

6x       a³b²

Los términos pueden estar compuestos por varios factores, y no una sola letra o número. Pero todos deben ser cuadrados.

Tercer caso(trinomio cuadrado perfecto):

En un trinomio cuadrado perfecto.

Regla para conocer si un trinomio es cuadrado perfecto.

1)	Un trinomio ordenado con relación a una letra
2)	Es cuadrado perfecto cuando el primer y tercer término son cuadrados perfectos
3)	El segundo término es el doble producto de sus raíces cuadradas.

Procedimiento para factorizar

1)	Se extrae la raíz cuadrada del primer y tercer término; en el ejemplo a y b.
2)	Se forma un producto de dos factores binomios con la suma de estas raíces; entonces (a + b)(a + b).
3)	Este producto es la expresión factorizada (a + b)2.

Si el ejercicio fuera así:

a2	-	2ab	+	b2	=	(a - b) 2
a				b

Procedimiento para factorizar

1)	Se extrae la raíz cuadrada del primer y tercer término; en el ejemplo a y b.
2)	Se forma un producto de dos factores binomios con la diferencia de estas raíces; entonces
	(a - b)(a - b).
3)	Este producto es la expresión factorizada (a - b)2.

Ejemplo 1: Factorizar x² + 10x + 25

La raíz cuadrada de : x² es x

La raíz cuadrada de : 25 es 5

El doble producto de las raíces: 2(x)(5) es 10x

Luego

x2 + 10x + 25

=

(x + 5)2

Ejemplo 2: Factorizar 49y² + 14y + 1

La raíz cuadrada de : 49y² es 7y

La raíz cuadrada de : 1 es 1

El doble producto de las raíces: 2(7y)(1) es 14y

Luego

49y2 + 14y + 1

=

(7y + 1)2

Ejemplo 3: Factorizar 81z² - 180z + 100

La raíz cuadrada de : 81z² es 9z

La raíz cúbica de : 100 es 10

El doble producto de las raíces: 2(9z)(10) es 180z

Luego

81z2 - 180z + 100

=

(9z - 10)2

		4a8		32a4b
Ejemplo 4:	Factorizar	---	-	------			+	64b2
		49		7

	4a8		2a4
La raíz cuadrada de :	--	es	--

Maximo Comun Divisor

Máximo común divisor

El mayor número por el que se pueden dividir dos o más números.

Si se encuentran todos los factores de dos o más números y se encuentra que algunos factores son los mismos ("Comunes"), entonces el mayor de estos factores comunes es el Máximo Común Divisor.

Cálculo del máximo común divisor

1 Se descomponen los números en factores primos.

2 Se toman los factores comunes con menor exponente.

3 Se multiplican dichos factores y el resultado obtenido es el mcd.

Ejemplo de cálculo de máximo común divisor

Hallar el m. c. d. de: 72, 108 y 60:

1 

Solución: 

72 = 2³ · 3²

108 = 2² · 3³

60 = 2² · 3 · 5

2 m. c. d. (72, 108, 60) = 2² · 3 = 12

12 es el mayor número que divide a 72, 108 y 60.

Propiedades del máximo común divisor

1 Los divisores comunes de varios números coinciden con los divisores del máximo común divisor.

Ejemplo: 

Calcular los divisores comunes de 54 y 90.
m.c.d (54, 90) = 18
Los divisores comunes de 54 y 90 son los divisores de 18, por tanto serían 1, 2, 3, 6, 9, 18.

2 Dados varios números, si se multiplican o dividen por otro número entonces su
m.c.d también queda multiplicado o dividido por el mismo número.

Ejemplo: 

m.c.d. (54, 90) = 18
Si multiplicamos los dos números por 3 queda:

54 · 3 = 162

90 · 3 = 270

m.c.d. (162, 270) = 54 = 18 · 3

3 Esta propiedad es consecuencia de la anterior: Dados varios números, si se dividen por su m.c.d los cocientes resultantes son primos entre sí (su m.c.d es 1).

Ejemplo: 

m.c.d. (54, 90) = 18

54: 18 = 3

90: 18 = 5

m.c.d. (3, 5) = 1

4 Si un número es divisor de otro, entonces este es el m. c. d de los dos.

Ejemplo: 

El número 12 es divisor de 36.

m.c.d. (12, 36) = 12

HERRAMIENTA PARA CALCULAR Y VERIFICAR

http://es.onlinemschool.com/math/assistance/number_theory/nod_nok/

Minimo Comun Multiplo

Mínimo común múltiplo

¿Qué es un "múltiplo"?

Los múltiplos de un número son lo que tienes cuando lo multiplicas por otros números (si lo multiplicas por 1, 2,3,4,5, etc.) como en las tablas de multiplicar.

Aquí tienes ejemplos:

Los múltiplos de 3 son 3, 6, 9, 12, 15, 18, 21, etc...

Los múltiplos de 12 son 12, 24, 36, 48, 60, 72, etc...

¿Qué es un "múltiplo común"?

Si tienes dos (o más) números, y miras entre sus múltiplos y encuentras el mismo valor en las dos listas, esos son los múltiplos comunes a los dos números.

Por ejemplo, si escribes los múltiplos de dos números diferentes (digamos 4 y 5) los múltiplos comunes son los que están en las dos listas:

Los múltiplos de 4 son 4,8,12,16,20,24,28,32,36,40,44,...

Los múltiplos de 5 son 5,10,15,20,25,30,35,40,45,50,...

¿Ves que 20 y 40 aparecen en las dos listas? Entonces, los múltiplos comunes de 4 y 5 son: 20, 40 (y 60, 80, etc. también)

¿Qué es el "mínimo común múltiplo"?

Es simplemente el más pequeño de los múltiplos comunes. En el ejemplo anterior, el menor de los múltiplos comunes es 20, así que el mínimo común múltiplo de 4 y 5 es 20.

Calcular el mínimo común múltiplo

En realidad es muy fácil de hacer. Sólo escribe los múltiplos de los números hasta que encuentres uno que coincida.

Ejemplo 1: encuentra el mínimo común múltiplo de 3 y 5:

Los múltiplos de 3 son 3, 6, 9, 15, ..., y los múltiplos de 5 son 5, 10, 15, 20, ..., así:

Como puedes ver en esta línea de números, el primer múltiplo que coincide es el 15. Respuesta: 15

Y puedes calcular el mínimo común múltiplo de 3 (o más) números.

Ejemplo 2: calcula el mínimo común múltiplo de 4, 6 y 8

Los múltiplos de 4 son: 4, 8, 12, 16, 20, 24, 28, 32, 36, ... Los múltiplos de 6 son: 6, 12, 18, 24, 30, 36, ... Los múltiplos de 8 son: 8, 16, 24, 32, 40, .... Entonces 24 es el mínimo común múltiplo de (¡no podemos encontrar uno más pequeño!)

Pista: puedes hacer listas más pequeñas de los números más grandes.

Herramienta para el mínimo común múltiplo

Hay otro método, puedes usar nuestra Herramienta para el mínimo común múltiplo para calcularlo automáticamente.

El mínimo común múltiplo es el menor de todos los múltiplos comunes de varios números, excluido el cero.

Cálculo del mínimo común múltiplo

1 Se descomponen los números en factores primos.

2 Se toman los factores comunes y no comunes con mayor exponente.

Ejemplos:

Hallar el m.c.m. de 72, 108 y 60:

72 = 2³ · 3²

108 = 2² · 3³

60 = 2² · 3 · 5

Solución: 

m.c.m. (72, 108, 60) = 2³ · 3³ · 5= 1080

1 080 es el menor múltiplo común a 72, 108 y 60.

1 080 es el menor número que puede ser dividido por 72, 108 y 60.

Propiedades del mínimo común múltiplo

1 Dados varios números todo múltiplo común a ellos es múltiplo del m.c.m de dichos números.

2 Los múltiplos comunes a varios números son también múltiplos del m.c.m de dichos números.

Ejemplo:

m.c.m. (16, 8) = 80

Algunos de los múltiplos comunes de 16 y 8 son 160, 240, 320 que también son múltiplos de 80

3 Cualquier múltiplo del m.c.m. de varios números también lo es de dichos números.

Ejemplo:

m.c.m. (16, 8) = 80

Algunos de los múltiplos de 80 son 160, 240, 320 que también son múltiplos de 16 y de 8

4El m.c.m. de dos números primos entre sí es su producto.

Ejemplo:

m.c.m (2,5) = 2 · 5 = 10

5Si un número es un múltiplo de otro, entonces es el m. c. m. de ambos.

Ejemplo:

El número 36 es múltiplo de 12.

m. c. m. (12, 36) = 36

6Dados varios números, si se multiplican o dividen por otro número entonces su m.c.m también queda dividido o multiplicado por el mismo número.

Ejemplo:

m.c.m. (32, 84) = 672

32 · 4 = 128

84 · 4 = 336

m.c.m (128, 336) = 2688 = 672 · 4