Sistemas de
numeración
Un Sistema de Numeración, es un conjunto de reglas y
principios, que se emplean para representar correctamente los números. Entre
estos principios tenemos
Entre estos principios tenemos:
1. Principio de
Orden
2. Principio de la Base
3. Principio posicional
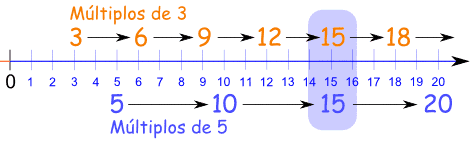
v Principio de orden
Sistema de
numeración en base 2
El sistema binario, en matemáticas e informática, es
un sistema de numeración en el que los números se representan utilizando
solamente las cifras cero y uno (0 y 1). Es el que se utiliza en las
computadoras, debido a que trabajan internamente con dos niveles de voltaje,
por lo que su sistema de numeración natural es el sistema binario (encendido 1,
apagado 0).
Ejemplo
|
Transformar el número decimal 100 en
binario. El método de la operación es muy simple:
|
|
|
el
número decimal 131 en binario. El método es muy simple:
|
131
dividido entre 2 da 65 y el resto es igual a 1
 65 dividido entre 2 da 32 y el resto es
igual a 1
32 dividido entre 2 da 16 y el resto es
igual a 0
16 dividido entre 2 da 8 y el resto es igual a 0
8 dividido entre 2 da 4 y el resto es igual a 0
4 dividido entre 2 da 2 y el resto es igual a 0
2 dividido entre 2 da 1 y el resto es igual a 0
1 dividido entre 2 da 0 y el resto es igual a 1
-> Ordenamos los restos, del último al
primero que estan en color Azul: 100000112
|
En sistema
binario, 131 se escribe 100000112
Sistema de numeración en base 3
|
El sistema ternario es
el nombre que se le da a la base 3 constante.
Para representar cualquier número en
el sistema ternario, se utilizan los dígitos del 0, 1, 2.
Conversión
entre el Sistema Ternario y el Sistema Decimal
Decimal a
Ternario
Se divide el
número del sistema decimal entre 3,
cuyo resultado entero se vuelve a dividir entre 3, y así
sucesivamente. Ordenados los restos, del último al primero, éste será el
número Ternario que buscamos
el número
decimal 5431 en Ternario. El método es muy simple:
|
5431
dividido entre 3 da 1810 y el resto es
igual a 1
1810
dividido entre 3 da 603 y el resto es igual a 1
603 dividido entre 3 da 201
y el resto es igual a 0
201 dividido entre 3 da 67
y el resto es igual a 0
67 dividido entre 3 da 22
y el resto es igual a 1
22 dividido entre 3 da 7
y el resto es igual a 1
7 dividido entre 3 da 2
y el resto es igual a 1
2 dividido entre 3 da 0
y el resto es igual a 2
R/
Ordenamos los restos, del último al primero que estan de colores: 211100113
|
En sistema Ternario, 5431 se
escribe 211100113
|
Ejemplo 2
|
Transformar el
número decimal 5431 en ternario. Este método es el másutilizado para la
operación que el anterior:
|
|
|
Para este
Ejemplo se toman en:
* Primer lugar el cociente, que es 2
* Segundo lugar todos los residuos(restos) de la división.
Nos queda que el Número Decimal 5431, se escribe en el sistema ternario
como 211100113
|
El sistema
quinario es el nombre que se le da a la base 5 constante. Este sistema tiene su
origen en el hecho de que los humanos tienen cinco dedos en cada mano, por lo
que es uno de los sistemas de numeración más antiguos.
Para
representar cualquier número en el sistema quinario, se utilizan los dígitos
del 0, 1, 2, 3, 4. En el siglo XX, solamente ciertas tribus del este de África
seguían utilizando un sistema de base cinco. Sin embargo, el sistema de base
diez (decimal) ha prevalecido en la mayoría de los territorios y éstas tribus,
como todas las otras culturas que usaban el sistema quinario, se han convertido
a él.
Conversión entre el Sistema Quinario y
el Sistema Decimal
DECIMAL A QUINARIO
Se divide el número del
sistema decimal entre 5, cuyo resultado entero se vuelve a dividir entre
5, y así sucesivamente. Ordenados los restos, del último al primero, éste será
el número Quinario que buscamos
Ejemplo 1
|
Transformar
el número decimal 131 en Quinario. El método es muy simple:
|
131
dividido entre 5 da 26 y el resto es igual a 1
26 dividido entre 5 da 5 y el resto es igual a 1
5 dividido entre 5 da 1 y el resto es igual a 0
1 dividido entre 5 da 0 y el resto es igual a 1
R/ Ordenamos los restos, del último al
primero que estan en colores: 11015
|
Ejemplo
2
|
Transformar el número decimal 100
en binario. El método de la operación es muy simple:
|
|
|
En sistema binario, 100 se
escribe 11001002
Sistema de numeración en base 8
El sistema Octal
El sistema numérico en base 8 se llama octal y
utiliza los dígitos 0, 1, 2. 3. 4, 5, 6, 7.
Por ejemplo, el número 74 (en decimal) es 1001010 (en binario), lo
agruparíamos como 1 / 001 / 010, de tal forma que obtengamos una serie de
números en binario de 3 dígitos cada uno (para fragmentar el número se
comienza desde el primero por la derecha hacia la izquierda y se parte de 3
en 3), después obtenemos el número en decimal de cada uno de los
números en binario obtenidos: 1=1, 001=1 y 010=2. De modo que el número decimal 74
en octal es 112.
Hay que hacer notar que antes de poder pasar un número a octal es necesario
pasar por el binario. Para llegar al resultado de 74 en octal se
sigue esta serie: decimal -> binario -> octal.
En informática, a veces se utiliza la numeración octal en vez de la hexadecimal.
Tiene la ventaja de que no requiere utilizar otros símbolos diferentes de los
dígitos. Sin embargo, para trabajar con bytes o conjuntos de ellos,
asumiendo que un byte es una palabra de 8 bits, suele ser más
cómodo el sistema hexadecimal, por cuanto todo byte así definido es
completamente representable por dos dígitos hexadecimales.
Es posible que la numeración octal se usara en el pasado en lugar del decimal, por
ejemplo, para contar los espacios interdigitales o los dedos distintos de los
pulgares.
Conversión entre el Sistema Octal y el Sistema Decimal
DECIMAL A OCTAL
Tenemos dos formas de realizar la
conversión:
a) dividir el número decimal entre 8, cuyo resultado entero
se vuelve a dividir entre 8, y así sucesivamente.
b) pasar el número decimal a binario y posteriormente este
número binario a octal (en este proceso podemos observar la influencia
de los binarios en los octal y viceversa).
Iniciemos nuestra conversión con la forma a) la cual costa de
divisiones sucesivas.
Transformar el número decimal 131 en número Octal.
|
Solución
|
Pero en Primer Lugar realicemos las divisiones sucesivas.
|
|
|
En segundo
lugar ordenamos los residuos y el último cociente, para obtener la
respuesta en el sistema octal. Entonces 131 se escribe 2038
|
|
Sistema de numeración en base 10
El sistema decimal es
un sistema de
graduación posicional en el que las cantidades se
representan utilizando como base el número diez,
por lo que se compone de diez cifras diferentes: cero (0); uno (1); dos (2); tres (3);cuatro (4); cinco (5); seis (6); siete (7); ocho (8)
y nueve (9).
Este conjunto de símbolos se denomina números árabes, y es de origen hindú.
Excepto en ciertas culturas, es el sistema de posición usado habitualmente en
todo el mundo y en todas las áreas que requieren de un sistema de numeración.
Sin embargo hay ciertas técnicas, como por ejemplo en la informática,
donde se utilizan sistemas de numeración adaptados al método de trabajo como
el binario o el hexadecimal. También pueden existir en algunos
idiomas vestigios del uso de otros sistemas de numeración, como el quinario, el duodecimal y el vigesimal. Por ejemplo, cuando se cuentan
artículos por docenas, o cuando se emplean palabras especiales para designar ciertos
números; en francés, por ejemplo,
el número 80 se expresa «quatre-vingt», «cuatro veintenas», en español.
Según los antropólogos, el origen del sistema decimal está
en los diez dedos que tenemos los humanos en las manos, los cuales siempre
nos han servido de base para contar.
El sistema decimal es un sistema de numeración posicional, por
lo que el valor del dígito depende de su posición dentro del número.
Así:
Ejemplo 1
|
Pasemos el número 528 del Sistema
de Numeración Decimal a la Forma Extensa (escrito en Base
10).
|
528
|
|
= 5x100 + 2x10 + 8
|
=>
|
También se lee 5 veces 100 + 2 veces
10 + 8
|
= 5x102 + 2x101 + 8
|
|
|
Escrito en forma extensa, equivale a:
528 = 5x102 + 2x101 + 8
|
Ejemplo 2
|
Pasemos el
número 3684 del Sistema de Numeración Decimal a laForma
Extensa (escrito en Base 10).
|
3684
|
|
= 3x1000 +
6x100 + 8x10 + 4
|
=>
|
También
se lee 3 veces 1000 + 6 veces 100 + 8 veces 10 + 4
|
= 3x103 +
6x102 + 8x101 + 4
|
|
|
Escrito en
forma extensa, equivale a:
|
3684 = 3x103 +
6x102 + 8x101 + 4
|
Ejemplo 3
|
Pasemos el
número 15200 del Sistema de Numeración Decimal a laForma
Extensa (escrito en Base 10).
|
15200
|
|
= 1x10000 +
5x1000 + 2x100 + 0x10 + 0
|
=>
|
También
se lee 1 veces 10000 + 5 veces 1000 + 2 veces 100 + 0 veces 10 + 0
|
= 1x104 +
5x103 + 2x102 + 0x101 + 0
|
|
|
Escrito en
forma extensa, equivale a:
|
15200 = 1x104 +
5x103 + 2x102 + 0x101 + 0
|
|
|
Sistema de numeración
en base 16
El sistema
Hexadecimal (no confundir con sistema
sexagesimal), a veces abreviado como Hex, es el sistema de
base 16 —empleando por tanto 16 símbolos—. Su uso actual está
muy vinculado a la informática y ciencias de la computación, pues los computadores suelen
utilizar el byte u
octeto como unidad básica de memoria; y, debido a que
un byte representa 28 valores posibles, y esto puede representarse
como
, que, según
el teorema general de la numeración posicional, equivale al número en base
16 10016, dos dígitos hexadecimales corresponden exactamente —permiten
representar la misma línea de enteros— a un byte.
En principio dado que el sistema usual de numeración es de base decimal y, por ello, sólo se dispone de
diez dígitos, se adoptó la convención de usar las seis primeras letras del
alfabeto latino para suplir los dígitos que nos faltan. El conjunto
de símbolos sería, por tanto, el siguiente:
S =
{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}
Se debe
notar que A = 10, B = 11, C = 12, D = 13, E = 14 y F = 15. En ocasiones se
emplean letras minúsculas en lugar de mayúsculas. Como en cualquier sistema de
numeración posicional, el valor numérico de cada dígito es alterado dependiendo
de su posición en la cadena de dígitos, quedando multiplicado por una cierta
potencia de la base del sistema, que en este caso es 16. Por ejemplo: 3E0A16 =
3×163 + E×162 + 0×161 + A×160 = 3×4096 + 14×256 + 0×16 +
10×1 = 15882.
El sistema hexadecimal actual fue introducido en el ámbito de la computación
por primera vez por IBM en 1963. Una representación anterior, con 0–9 y u–z, fue
usada en 1956 por
la computadora Bendix G-15.
Conversión entre el Sistema Hexadecimal y el Sistema Decimal
DECIMAL A HEXADECIMAL
Tenemos dos
formas de realizar la conversión:
a) dividir el número decimal entre 16, cuyo resultado entero
se vuelve a dividir entre 16, y así sucesivamente.
b) pasar el número decimal a binario y posteriormente este numero binario
a hexadecimal (en este proceso podemos observar la influencia de los
binarios en los hexadecimal y viceversa).
Iniciemos nuestra conversión con la forma a) la cual costa de
divisiones sucesivas.
Ejemplo 1
|
Transformar
el número decimal 131 en número Hexadecimal.
|
Solución
|
Pero en Primer Lugar realicemos las divisiones sucesivas.
|
|
|
En segundo lugar ordenamos
los residuos y el último cociente, para obtener la respuesta en el
sistema hexadecimal. Entonces 131 se escribe 8316
Ejemplo
2
|
Transformar
el número decimal 100 en número Hexadecimal.
|
Solución
|
Pero en Primer Lugar realicemos las divisiones sucesivas.
|
|
|
En segundo lugar ordenamos
los residuos y el último cociente, para obtener la respuesta en el
sistema hexadecimal. Entonces 100 se escribe 6416
|
|
Sistema de numeración en base 60
SISTEMA DE
NUMERACIÓN BABILÓNICA Babilonia fue una ciudad de la baja Mesopotamia y estaba
localizada en lo que es hoy Iraq. Este sistema apareció por primera vez
alrededor de 1800-1900 a. C. Es el primer sistema de numeración posicional, es
decir, en el cual el valor de un dígito particular depende tanto de su valor
como de su posición en el número que se quiere representar. Los números en este
sistema se representaban con la ayuda de sólo dos símbolos, una cuña vertical V
que representaba a la unidad y una cuña horizontal para el número diez. Estas
cuñas resaltaban en las tablillas de las cuñas de arcilla, por los palitos inclinados,
y tomaban la forma de un prisma. De aquí surgió la denominación de cuneiforme
para la escritura de los antiguos babilonios. 1 10 El sistema de numeración
babilónico es de base 60 (sexagesimal) y los números enteros del 1 al 59 se
podían escribir de manera que los signos para el diez y la unidad se repetían
tantas veces como en el número hubiese decenas y unidades. La unidad de segundo
orden representada por el mismo signo es 60 veces mayor que la de primer orden,
y la unidad de tercer orden es 60 veces mayor que la de segundo y 3600 veces
mayor (60 * 60 = 3600) que la unidad de primer orden. Y así sucesivamente. Este
sistema de numeración es posicional. Así, un mismo signo puede representar en
él, tanto 1 como 1 * 60, como 1*60*60 = 1 * 60 2 = 1 * 3600, etc., en función
del lugar en que dicho signo
Sistema de numeración en base 64
Base 64 es
un sistema de numeración posicional que usa 64 como base. Es la
mayor
potencia de dos que puede ser representada usando únicamente los
caracteres imprimibles de ASCII. Esto ha propiciado su uso para codificación de correos electrónicos, PGP y otras
aplicaciones. Todas las variantes famosas que se conocen con el nombre de
Base64 usan el rango de caracteres A-Z, a-z y 0-9 en este orden para los
primeros 62 dígitos, pero los símbolos escogidos para los últimos dos dígitos
varían considerablemente de unas a otras. Otros métodos de codificación como UUEncode y
las últimas versiones de binhex usan un conjunto diferente de 64 caracteres para
representar 6 dígitos binarios, pero estos nunca son llamados Base64.
Cálculo del máximo común divisor
2 Dados varios números, si se multiplican o
dividen por otro número entonces su
